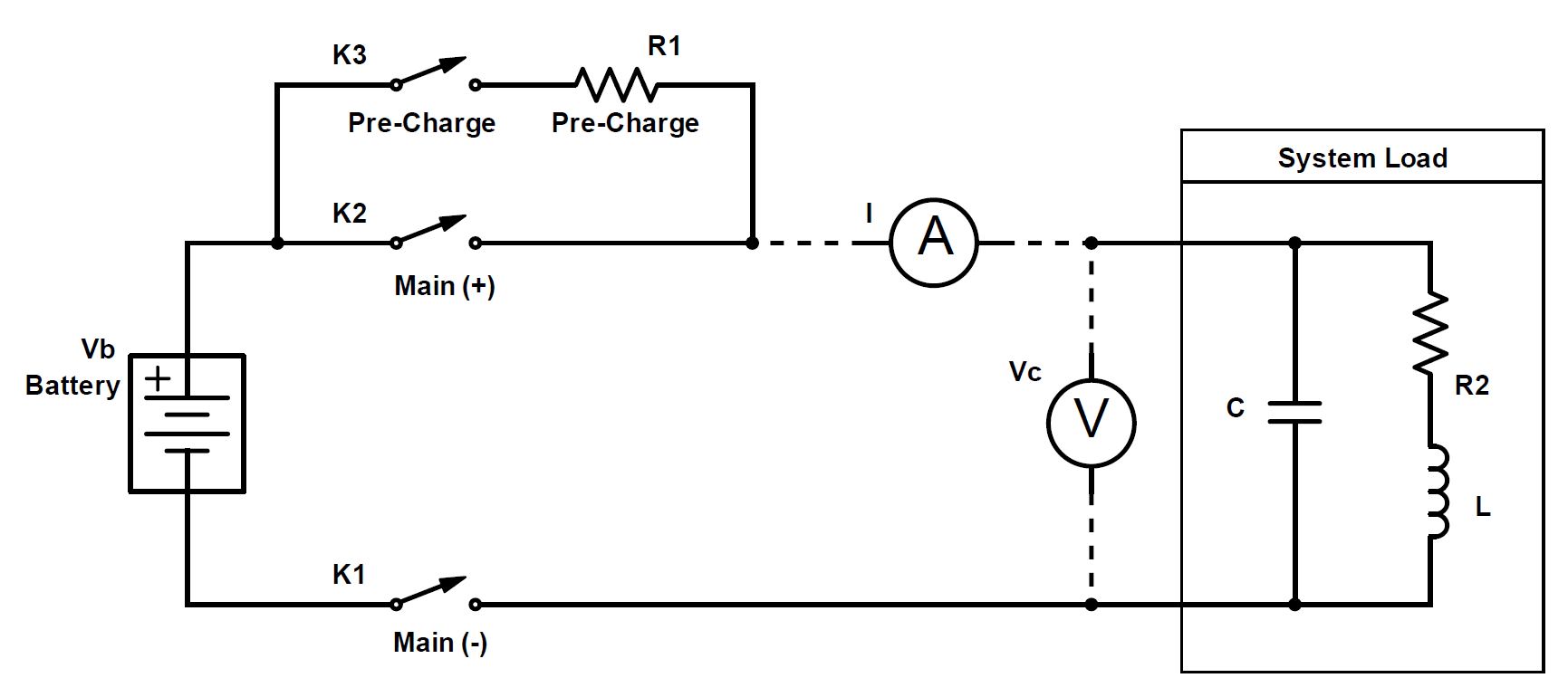
定义
| 欧拉常数 | e | 2.71828 | 数值常数。 |
| 电池电压 | Vb | 系统/电池电压 (DC)。 | |
| 已用时间 | t | 预充电开始后已过去的时间。 | |
| 所需预充电时间(最大值) | T_{max} | 使系统达到所需充电水平可接受的最长时间。 | |
| 期望预充电百分比 | q | 关闭主接触器前所需系统电容的充电百分比。 | |
| 系统电容 | C | 需要预充电的系统/负载电容。 | |
| 所需时间常数数值 | n | n=-ln|1-q| | 将负载电容预充电至所需百分比所需的时间常数值。 |
| 最大预充电电阻 | R_{1,max} | R_{1,max} = \frac {T_{max}} {nC} | 在所需时间内将负载电容充电至所需电平的最大预充电电阻。所用的实际预充电电阻可以小于该值,这会加快预充电速度,但通过电阻的功耗也会更高。 |
| 选定的电阻值 | R_1 | 选定的预充电电阻值。通过勾选该框可以使用上面计算出的最大电阻,但也可以使用任何其他值,例如,试验市场上很容易买到的电阻,或尝试更快地进行预充电。 | |
| 主电路中的总串联电阻 | R_2 | 主电路中负载的总电阻、导体、开关和连接器的接触电阻等。通过以下操作确定:当您的系统完全组装和连接,正极主接触器 (K_2) 处于断开状态,负极主接触器 (K_1) 和预充电接触器 (K_3) 处于闭合状态时,使用欧姆表测量正极主接触器 (K_2) 电源端子之间的电阻。这用于确定预充电完成后主接触器 (K_2) 闭合时通过主接触器的涌入电流。R_2 应该比 R_1 小得多,否则就不需要预充电电路。 | |
| 时间常数 | τ | τ=R_1C | RC 电路的时间常数。这是将电容器充电到 63.2% SOC 所需的时间。对于给电容完全充电而言,五倍时间常数是一个很好的经验法则。否则,主接触器可能会存在焊接风险。这可以通过更改预充电时间输入 "T_{max}" 进行调整。 |
| 实际预充电时间 | T | T = nR_1C | 使用选定的电阻值将系统预充电至所需电平所需的实际时间。如果使用 R1max,该时间应等于所需的预充电时间输入。 |
| 预充电电路涌入电流 | I(0) | I(t) = \frac{V_b}{R_1}e^ \frac{-t}{R_1C} 在 t=0 时评估 I(0) = \frac{V_b}{R_1} |
t=0 时的峰值电流,正好在预充电接触器闭合时。这对于检查预充电接触器在负载下闭合的能力很重要。每次对系统进行预充电时,预充电接触器都需要闭合到该电流。 |
| 电容电压 | V_c(t) | V_c(t) = V_b(1-e^{\frac{-t}{R_1C}}) | 在开始预充电之后的时间“t”跨越负载电容的电压。该值随电容充电而增加。 |
| 预充电电阻消耗的电能 | E(T) | E(t) = \frac{CV_b^2}{2}(1-e^{\frac{-2t}{R_1C}}) 在 t=T 时评估 E(\infin) = \frac{CV_b^2}{2} |
预充电过程中预充电电阻消耗的累积电能。如果预充电时间非常大(>5 倍时间常数),则这将接近 \frac{CV_b^2}{2},这等于电容充满电时存储在电容中的总电能。 |
| 功率 | P(t) | P(t) = I(t)^2R_1 | 预充电开始后,在时间“t”通过电阻消耗的功率。 |
| 平均功率 | P_{avg} | P_{avg} = \frac{E(T)}{T} | 预充电电阻消耗的总电能除以实际预充电时间。选择预充电电阻时,确保它可以在“T”时间内处理“P_{avg}”。 |
| 峰值功率 | P_p | P_p = I(0)^2R_1 | 预充电电阻将看到的峰值瞬时功率。这发生在预充电接触器闭合的瞬间。选择预充电电阻时,确保它能在很短的时间 \lll T 内处理 "P_p"。 |
| 预充电后剩余电压增量 | V_d(T) | V_d(t) = V_b-V_c(t) V_d(t) = V_be^{\frac{-t}{R_1C}} 在 t=T 时评估 |
预充电后主接触器两端剩余的电压降。这与主电路中的串联电阻一起,将决定主接触器闭合时通过主接触器的涌入电流。 |
| 预充电后主接触器涌入电流 | I_m | I_m = \frac{V_d(T)}{R_2} | 一旦预充电完成,这是主接触器闭合时将暴露的涌入电流。 |
本文提供的结果仅供参考。请联系森萨塔应用工程部门检查计算结果并协助产品选择。